Laplace transformation method on the basis of pulse wave form in a laser flash method
Kazuya HOSONO , Toshinori DOZONO
Japan ultra-high Temperature Materials Research Institute, 573-3
Okiube,Ube,Yamaguchi 755, Japan
ABSTRACT
ABSTRACT
The laser flash method is considered as the andard and the most popular one for thermal
diffusivity measurement of solid materials. According to the irradiation time of the flash,the flash is usually approximated to concentra-te at the center of gravity. In laplace trans-formation analysis(LTA), method taking accout of pulse wave form was given by Tailor et al.侾乯,in case of no heat loss. Two methods of taking
account of pulse wave form and heat loss have been developed in LTA. The procedures of the LTA are as follows.
乲method No.1:cooling time constant method乴
1. The cooling region of the experimental curve is fitted by an exponential curve and the cooling time constant 冄 is calculated. In this region, first term of eq.(1) must be dominant and other terms are negligible.
2. Biot number h is obtained using eq.(6).
3. Experimental temperature and pulse data are transformed using eq.(4)-(5).
4. Thermal diffusivity 兛 is determined by seek- ing the minimum of the least-squares function eq.(7) or (8).
5. 兛 and h are determined by iteration of 2.and 4.
乲method No.2:direct method乴
1. Experimental temperature and pulse data are transformed using eq.(4)-(5).
2. Thermal diffusivity 兛 and biot number h are determined by seeking the minimum of the least-squares function eq.(9) or (10).
Theoretical data were obtained using eq.(1)-(2) in order to confirm these methods. Pulse
wave form is saw tooth of 1 ms duration (pulse width :t倫倵) and sampling period is 1 兪s. Samp-le data are as follows.乲兛: 1.0亊10-4 m俀/s, L:0.497乣2.433 mm, t侽: 0.25乣6.00ms (t侽=L俀/(兾<>俀兛)),h: 0.01 乣0.80, t倱(sampling period): 2.0 乣 10.0兪s乴
Fig.1 shows the errors of 兛 and h using eq.(7). The errors of 兛 and h are almost the same that each point overlaps. The present method shows the error less than 1% for all data. On the other hand, the method of center of gravityshows that the errors of 兛 and h increase as the characteristic time/pulse width t侽/t倫倵 dec-reases especially less than 3. Similar results are given in the case of other biot number and also using eq.(8).
Fig.2 shows the relation be-tween pt倣倝値 and errors of 兛 and h using data(兛=1.0亊10-4 m俀/s,h=0.01,t侽=6.00ms).Pt倣倝値 in the range of 7 乣323 gives 兛 and h less than 1% accuracy.
Fig.3 shows the result of 兛 and h accuracy using eq.(9)-(10). Similar results aregiven for other biot number data. Fig.4 shows the relation between the amount of data and the accuracies of 兛 and h. The amount of data is set by t侽亊m/t倱 + n侽(m:integer, n侽:number of 0 data). In this case,the 兛 accuracy is less than 1% for m 亞 2.
NOMENCLATURE
倲 : time
俴 : thickness of a specimen
兛 : thermal diffusivity of a specimen
倛 : biot number of a specimen
冄 : cooling time constant of a specimen
倲侽 : characteristic time of a specimen
俿(倲) : temperature rise of rear surface of a specimen
俿M : maximum 俿(倲) without heat losses
倫 : laplace transformation variable
倖(t) : normalized pulse wave form
儗乕僓僼儔僢僔儏朄偵偍偗傞僷儖僗攇宍傪峫椂偟偨儔僾儔僗嬻娫夝愅朄
仜嵶栰榓栫乮挻崅壏嵽尋媶強乯丂摪墍棙摽乮挻崅壏嵽尋媶強乯
侾丏弿尵
儗乕僓僼儔僢僔儏朄偵偍偗傞僷儖僗攇宍偵娭偡傞庢埖偄偼丄庡偲偟偰僷儖僗偺廳怱埵抲偵慡僄僱儖僊乕偑廤拞偟偰偄傞偲嬤帡偟偨夝愅偱偁傞丅傑偨儔僾儔僗嬻娫偵偍偗傞夝愅朄偱丄擬曻幩懝幐偑柍偄応崌偵偮偄偰僷儖僗攇宍傪峫椂偟偨夝愅朄偑曬崘侾乯偝傟偰偄傞丅摿惈帪娫偑僷儖僗暆偵斾妑偟偰彫偝偄帋椏偱偼僷儖僗廳怱嬤帡偑惉棫偣偢丄傑偨擬曻幩懝幐傪峫椂偟側偄偲擬奼嶶棪傪惛搙椙偔夝愅偡傞偙偲偼偱偒側偄丅杮尋媶偱偼丄埲忋偺栤戣傪夝寛偡傞偨傔偵儔僾儔僗嬻娫偵偍偄偰擬曻幩懝幐偍傛傃僷儖僗攇宍傪嫟偵峫椂偟偨夝愅朄傪専摙偟偨丅杮専摙偵偍偄偰偼師偺忦審傪壖掕偟丄堦師尦擬揱摫偑惉棫偡傞傕偺偲偟偨丅
丂丂乮侾乯僷儖僗岝尮偼丄帋椏昞柺傪嬒堦偵壛擬偡傞丅
丂丂乮俀乯帋椏偼嬒幙偱偁傝丄應掕拞擬奼嶶棪偼堦掕偱偁傞丅
丂丂乮俁乯帋椏偐傜偺擬懝幐偼昞柺壏搙偵斾椺偟丄帋椏昞棤柺偺價僆乕悢偼摍偟偄丅
俀丏堦師尦擬揱摫曽掱幃偺棟榑夝
擬奼嶶棪兛丄岤偝俴偺帋椏偵攇宍俻倖乮倲乯偺儗乕僓僷儖僗偑倶亖侽柺偵徠幩媧廂偝傟偨偲偒丄帋椏棤柺倶亖俴偺帪娫嬻娫偵偍偗傞壏搙忋徃俿乮俴丆倲乯偼幃乮侾乯偱丄儔僾儔僗嬻娫偵偍偗傞壏搙忋徃俿乮俴丆P乯偼乮俁乯幃偱帵偝傟傞丅偙偙偵俿俵偼丄擬曻幩懝幐偑柍偄応崌偺帋椏嵟崅壏搙忋徃偱偁傝丄P偼儔僾儔僗曄悢偱偁傞丅
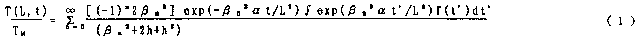
偙偙偵兝値偼屌桳抣偱偁傝師幃偱梌偊傜傟傞丅
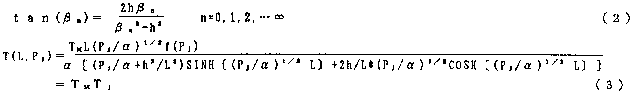
俁丏應掕僨乕僞偺儔僾儔僗曄姺
傑偢應掕僨乕僞傪俤乮倲乯偲偟偰師幃偵傛傝儔僾儔僗曄姺偡傞丅
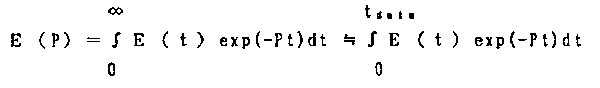 偙偙偵倲倓倎倲倎偼應掕僨乕僞偺庢傝崬傒帪娫偱偁傞丅壏搙僨乕僞偲僷儖僗僨乕僞偱偼偙偺倲倓倎倲倎偑堦斒偵堎側傞偑丄壏搙僨乕僞偺曽偑捠忢戝偒偄偺偱壏搙僨乕僞偺倲倓倎倲倎傪嫟捠偵梡偄偰椉僨乕僞偺儔僾儔僗曄姺曄悢P傪師幃偵廬偭偰愝掕偡傞丅偙偙偱倫倲倣倝値丄倫倲倣倎倶偼丄P倲倓倎倲倎偺嵟彫抣丄嵟戝抣偱偁傝丄偙偺斖埻撪偵値屄偺儔僾儔僗曄悢傪愝掕偡傞丅
偙偙偵倲倓倎倲倎偼應掕僨乕僞偺庢傝崬傒帪娫偱偁傞丅壏搙僨乕僞偲僷儖僗僨乕僞偱偼偙偺倲倓倎倲倎偑堦斒偵堎側傞偑丄壏搙僨乕僞偺曽偑捠忢戝偒偄偺偱壏搙僨乕僞偺倲倓倎倲倎傪嫟捠偵梡偄偰椉僨乕僞偺儔僾儔僗曄姺曄悢P傪師幃偵廬偭偰愝掕偡傞丅偙偙偱倫倲倣倝値丄倫倲倣倎倶偼丄P倲倓倎倲倎偺嵟彫抣丄嵟戝抣偱偁傝丄偙偺斖埻撪偵値屄偺儔僾儔僗曄悢傪愝掕偡傞丅
P倲倓倎倲倎亖倫倲倣倝値亄乮倫倲倣倎倶亅倫倲倣倝値乯*倝乛乮値亅侾乯 倝亖侽丏丏丏値亅侾 乮俆乯
丂儔僾儔僗嬻娫偵偍偗傞夝愅朄偲偟偰師偺俀偮偺曽朄傪嵦梡偟偨丅
乮侾乯帪掕悢傛傝價僆乕悢傪寛傔傞曽朄乮帪掕悢朄乯
嘆僷儖僗廳怱埵抲傛傝嵟崅壏搙忋徃偺侾乛俀偵払偡傞帪娫倲侾乛俀傛傝丄擬奼嶶棪弶婜抣兛0傪媮傔傞丅
嘇偙偺擬揱摫尰徾偺摿惈帪娫倲0偲偟偰倲乼倲0 傪枮偨偟乮侾乯幃偺戞侾崁偺傒偺嬤帡偑惉棫偡傞帪娫椞堟丂偵偍偄偰帪掕悢傪寁嶼偡傞偨傔偵丄擬奼嶶棪弶婜抣兛0傪傕偲偵摿惈帪娫倲0傪寁嶼偟丄倠侾亙倠2側傞丂掕悢傪愝掕偟丄僷儖僗廳怱埵抲傪帪娫尨揰偲偟偰倲0亊倠1乣倲0亊倠2偺嬫娫偱帪掕悢冄傪寁嶼偡傞丅丂偨偩偟丄帪娫尨揰偼丄僷儖僗廳怱埵抲偲偡傞丅
嘊價僆乕悢弶婜抣偼丄擬奼嶶棪弶婜抣兛侽偍傛傃帪掕悢冄傪梡偄偰乮侾乯丄乮俀乯幃傛傝摫偐傟傞師幃偵廬丂偄寁嶼偡傞丅
丂丂兝侽俀亖俴俀乛乮兛侽冄乯丆倛侽亖兝侽乵侾乛倱倝値乮兝侽乯亅侾乛倲倎値乮兝侽乯乶 丂丂丂乮俇乯
嘋壏搙偍傛傃僷儖僗偺應掕僨乕僞傪乮係乯丄乮俆乯幃偵廬偭偰儔僾儔僗曄姺偡傞丅偙偺嵺帪娫偺尨揰偼丄丂僷儖僗攇宍偺棫偪忋偑傝傛傝慜偵庢傞丅
嘍僷儖僗攇宍傪儔僾儔僗曄姺偟偨倖乮Pj乯傪乮俁乯幃偺儔僾儔僗嬻娫棟榑幃偵擖傟丄偙偺棟榑壏搙偲應掕丂壏搙傪梡偄偰擇忔曃嵎俼傪寁嶼偡傞丅偙偺擇忔曃嵎偲偟偰師偺俀幃傪帋傒偨丅兟俼乛兟俿兝M亖侽傛傝摫偐丂傟傞幃傪乮俈乯丄乮俉乯幃偵戙擖偟偨擇忔曃嵎傪埲壓偱巊梡偡傞丅
俼亖儼乮俿M俿j亅俤j乯俀 乮俈乯
俼亖儼乲俴俶乮俿M俿j乯亅俴俶乮俤j乯乴俀 乮俉乯
嘐擬奼嶶棪偍傛傃價僆乕悢弶婜抣傪傕偲偵兟俼乛兟兛亖侽傪枮懌偡傞擬奼嶶棪傪僯儏乕僩儞朄偱寁嶼偡傞丅
嘑旝彮抣傪兠丄僯儏乕僩儞朄偵傛傞擬奼嶶棪憹暘傪仮兛偲偟偰乥仮兛乥乛兛亙兠傪敾掕偟丄惉棫偡傟偽寁丂嶼廔椆丄晄惉棫偺偲偒偼嘐偱媮傔偨擬奼嶶棪傪怴偟偄弶婜抣偲偟偰嘊丄嘐偺孞傝曉偟寁嶼傪峴偆丅
乮俀乯擇忔曃嵎偺嬌彫抣傪捈愙媮傔傞曽朄乮捈愙朄乯
嘆僷儖僗廳怱埵抲傛傝嵟崅壏搙忋徃偺侾乛俀偵払偡傞帪娫倲侾乛俀傛傝丄擬奼嶶棪弶婜抣兛侽傪媮傔傞丅
嘇壏搙偍傛傃僷儖僗偺應掕僨乕僞傪乮係乯丄乮俆乯幃偵廬偭偰儔僾儔僗曄姺偡傞丅偙偺嵺帪娫偺尨揰偼丄丂僷儖僗攇宍偺棫偪忋偑傝傛傝慜偵庢傞丅
嘊僷儖僗攇宍傪儔僾儔僗曄姺偟偨倖乮P倞乯傪乮俁乯幃偺儔僾儔僗嬻娫棟榑幃偵擖傟丄偙偺棟榑壏搙偲應掕丂壏搙傪梡偄偰帺忔曃嵎俼傪寁嶼偡傞丅偙偺擇忔曃嵎偲偟偰師偺俀幃傪帋傒偨丅兟俼乛兟俿俵亖侽傛傝摫丂丂偐傟傞幃傪乮俋乯丄乮侾侽乯幃偵戙擖偟偨擇忔曃嵎傪埲壓偱巊梡偡傞丅
俼亖儼乮俿俵俿倞亅俤倞乯俀 乮俋乯
俼亖儼乲侾乛乮俿俵俿倞乯亅侾乛乮俤倞乯乴俀 乮侾侽乯
嘋價僆乕悢弶婜抣傪暋悢屄愝掕偟丄擬奼嶶棪弶婜抣傪傕偲偵兟俼乛兟兛亖侽傪枮懌偡傞擬奼嶶棪傪媮傔傞丅
嘍暋悢偺價僆乕悢偲偦偺價僆乕悢偵懳墳偟偨擬奼嶶棪傪梡偄偰擇忔曃嵎俼傪偦傟偧傟寁嶼偡傞丅
嘐擇忔曃嵎俼傪嵟彫抣偲偡傞擬奼嶶棪偍傛傃價僆乕悢偑媮傔傞傕偺偱偁傞丅偙偙偱敾掕偼丄價僆乕悢娫妘丂仮倛偑旝彮抣兠偵懳偟仮倛亙兠傪枮懌偡傞偲偒寁嶼廔椆丄晄惉棫偺偲偒偼擇忔曃嵎俼傪彫偝偔偡傞曽岦丂偵怴偨側價僆乕悢乮仮倛new亝仮倛old乯傪愝掕偟丄嘋丄嘍偺孞傝曉偟寁嶼傪峴偆丅
係丏専摙偵梡偄偨棟榑僨乕僞
杮夝愅曽朄傪妋擣偡傞偨傔偵乮侾乯幃偺棟榑夝傪傕偲偵棟榑僨乕僞傪嶌惉偟偨丅僷儖僗攇宍偼丄嫎帟忬攇乮塃壓偑傝乯偲偟丄僷儖僗暆侾倣倱丄僒儞僾儕儞僌廃婜侾兪倱偲偟偨丅帋椏僨乕僞偼丄擬奼嶶棪傪
侾丏侽亊侾侽亅係乮倣2乛倱乯偵屌掕偟丄帋椏岤偝傪侽丏係俋俈乣俀丏係俁俁倣倣偺娫偱愝掕偟丄摿惈帪娫偲偟偰侽丏俀俆乣俇丏侽侽倣倱偲側傞傛偆偵偟偨丅傑偨價僆乕悢傪侽丏侽侾乣侽丏俉侽偺娫偵愝掕偟偨丅壏搙僨乕僞偼僒儞僾儕儞僌廃婜傪俀丏侽乣侾侽丏侽兪倱偺娫偱愝掕偟丄摿惈帪娫偲僷儖僗暆偺戝偒偄曽偺俀侽攞偲偟丄俀侽係俋屄偺侽揰傪娷傔偰栺侾俀侽侽侽乣侾俇侽侽侽屄偱偁傞丅
俆丏専摙寢壥
乮侾乯帪掕悢朄偵傛傞寁嶼惂搙
價僆乕悢偑侽丏侾侽偺僨乕僞偱乮俈乯幃偺擇忔曃嵎傪梡偄偨応崌偺夝愅寢壥傪俥ig.侾偵帵偡丅夝愅忦審偼丄擬奼嶶棪弶婜抣傪傕偲偵寁嶼偟偨摿惈帪娫偺侾俆乣俀侽攞偲偟丄儔僾儔僗曄姺曄悢偼倫倲倣倝値亖侾俀丆倫倲倣倎倶亖侾俇丆値亖俆偲偟偨丅僷儖僗廳怱偵慡僄僱儖僊乕傪廤拞偝偣傞夝愅朄偱偼丄摿惈帪娫乛僷儖僗暆偑俁傛傝彫偝偔側傞偲師戞偵惛搙偑棊偪傞偑丄杮夝愅朄偱偼侾亾傛傝椙偄惛搙偱擬奼嶶棪偍傛傃價僆乕悢傪媮傔傞偙偲偑偱偒偨丅懠偺價僆乕悢偺僨乕僞偵偮偄偰傕傎傏摨條偺寢壥偱偁偭偨丅傑偨乮俉乯幃偺擇忔曃嵎偵偮偄偰傕摨條偺寢壥偑摼傜傟偨丅
乮俀乯帪掕悢朄偵偍偗傞儔僾儔僗曄悢偺愝掕
擬奼嶶棪丄價僆乕悢偺寁嶼惛搙偼儔僾儔僗曄悢乮倫倲倣倝値丆倫倲倣倎倶丆値乯偺庢傝曽偵埶懚偡傞丅擬奼嶶棪兛亖侾丏侽亊侾侽亅係乮倣2乛倱乯丄價僆乕悢倛亖侽丏侽侾丄摿惈帪娫倲侽亖俇丏侽侽倣倱乮俴亖俀丏係俁俁倣倣乯偺僨乕僞傪梡偄偰倫倲倣倝値偲擬奼嶶棪偍傛傃價僆乕悢偺寁嶼惛搙偺娭學傪媮傔俥ig丏俀偵帵偡丅偙偺僨乕僞偺応崌丄俈亙倫倲倣倝値亙俁俀俁偺斖埻偱擬奼嶶棪偍傛傃價僆乕悢傪侾亾傛傝椙偄惛搙偱寁嶼偡傞偙偲偑偱偒偨丅倫倲倣倎倶偍傛傃値偵偮偄偰偼寁嶼惛搙偲偺憡娭偑庛偔丄倫倲倣倎倶偼倫倲倣倝値亄乮俀乣係乯掱搙偵丄値偼俀乣俆掱搙偵庢傟偽椙偄丅懠偺僨乕僞偵偮偄偰傕傎傏摨條偺寢壥偱偁偭偨丅兟娭悢宍偺僷儖僗攇宍嬤帡傪偡傞応崌丄倫倲倣倝値偺愝掕斖埻偼侾侽埲壓偲嫹偄丅
乮俁乯捈愙朄偵傛傞擬奼嶶棪偲價僆乕悢偺寁嶼惛搙
價僆乕悢偑侽丏侾侽偺僨乕僞偱乮俋乯丄乮侾侽乯幃偺擇忔曃嵎傪梡偄偨応崌偺夝愅寢壥傪俥ig.俁偵帵偡丅夝愅忦審偼丄儔僾儔僗曄姺曄悢傪倫倲倣倝値亖侾俁丆倫倲倣倎倶亖侾俇丆値亖俆偲偟偨丅杮夝愅朄偵傛傝擬奼嶶棪偍傛傃價僆乕悢傪侾亾傛傝椙偄惛搙偱媮傔傞偙偲偑偱偒偨丅價僆乕悢偼擬奼嶶棪傛傝傕惛搙偑埆偔丄價僆乕悢偑戝偒偄僨乕僞傎偳價僆乕悢傪惛搙椙偔寁嶼偱偒偨丅懠偺價僆乕悢偺僨乕僞偵偮偄偰傕傎傏摨條偺寢壥偱偁偭偨丅
乮係乯捈愙朄偵偍偗傞僨乕僞検偲擬奼嶶棪偲價僆乕悢偺寁嶼惛搙
偙偺夝愅曽朄偼帪掕悢傪昁梫偲偟側偄偨傔丄傛傝彮側偄僨乕僞検偱夝愅偑壜擻偱偁傞丅
擬奼嶶棪兛亖侾丏侽亊侾侽亅係乮倣俀乛倱乯丄價僆乕悢倛亖侽丏侾侽丄摿惈帪娫倲0亖俇丏侽侽倣倱乮俴亖俀丏係俁俁倣倣乯偺僨乕僞傪梡偄偰僨乕僞検傪曄偊偰寁嶼惛搙傪妋擣偟偨丅僷儖僗攇宍偺棫偪忋偑傝傪帪娫偺尨揰偲偟偰摿惈帪娫偺惍悢攞倣偺僨乕僞検傪庢傝崬傒丄擬奼嶶棪偲價僆乕悢傪夝愅偟偨寢壥傪俥ig.係偵帵偡丅儔僾儔僗曄姺曄悢偼丄乮俋乯幃偱倫倲倣倝値亖侾俆丆倫倲倣倎倶亖侾俉丆値亖俆丄乮侾侽乯幃偱倫倲倣倝値亖侾侾丆倫倲倣倎倶亖侾係丆値亖俆偲偟偨丅偙偺僨乕僞偺応崌丄摿惈帪娫偺俀攞偺僨乕僞検偱傕侾亾傛傝椙偄惛搙偱擬奼嶶棪傪夝愅偡傞偙偲偑偱偒偨丅摿惈帪娫乛僷儖僗暆偑彫偝偔側傞傎偳擬奼嶶棪傪侾亾傛傝椙偔夝愅偡傞偺偵昁梫偲側傞僨乕僞検倣偑憹壛偡傞孹岦偵偁傞丅
俇丏傑偲傔
2偮偺儔僾儔僗曄姺朄偵傛傝擬奼嶶棪偍傛傃價僆乕悢偺夝愅傪帋傒丄偲傕偵擬奼嶶棪傪1亾傛傝椙偄惛搙偱夝愅偱偒傞偙偲傪柧傜偐偵偟偨丅帪掕悢傪梡偄傞曽朄偵傛傟偽丄慡僨乕僞偵懳偟埨掕偟偰擬奼嶶棪丄價僆乕悢傪媮傔傞偙偲偑壜擻偱偁傞丅捈愙朄偼丄彮側偄僨乕僞検偱傕擬奼嶶棪傪夝愅偱偒丄摿惈帪娫乛僷儖僗暆亖6.00偺僨乕僞偱偼丄摿惈帪娫偺俀攞偺僨乕僞検偱擬奼嶶棪傪1亾傛傝椙偄惛搙偱夝愅偱偒傞偙偲傪妋擣偟偨丅
References
1)J.Gembarovic,R.E.Taylor:Int.J.Thermophysics,14(1993),297
|